Bitwise NOT (~)
The bitwise NOT operator is a unary operator, meaning, it works on only one operand. The NOT operator simply inverts every bit of the operand.
Sounds familiar?
If you remember from the last article, Flipping every bit of a binary number produces the One’s Complement of that number.
Hence, this operator is also called the Complement Operator.
The Truth Table
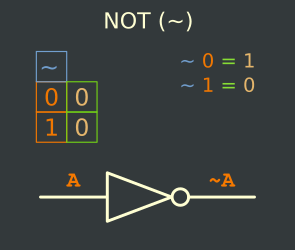
Examples :
~27
~0011011
= 1100100
~8
~1000
= 0111
So, as you could have guessed, the NOT operator is used to produce the Two’s Complement of a number.
Recalling from the previous article.
A Two’s Complement = One’s Complement + 1
Hence,
Two's Complement of 8 = ~8+1 = -8
Two's Complement of 27 = ~27+1 = -27
Bitwise AND (&)
The bitwise AND operator compares each bit of the first operand to the corresponding bit of the second operand. If both bits are 1, the corresponding result bit is set to 1, else the corresponding bit is set to 0.
The Truth Table
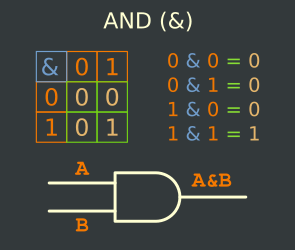
Examples :
47 & 84
00101111
& 01010100
-------------
00000100 = 4
27 & 10
00011011
& 00001010
-------------
00001010 = 10
Bitwise OR (|)
The bitwise OR operator compares each bit of the first operand to the corresponding bit of the second operand. If either of the bits is 1, the corresponding result bit is set to 1, else the corresponding bit is set to 0.
The OR operator is also called Inclusive OR operator because it includes as true the condition where both the inputs are true. ( 1 | 1 = 1 )
The Truth Table
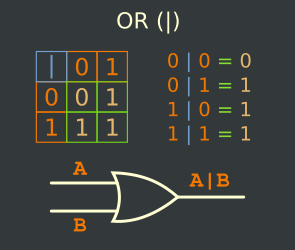
Examples :
27 | 10
00011011
| 00001010
-------------
00011011 = 27
12 | 10
1100
| 1010
-------------
1110 = 14
Bitwise XOR (^)
The bitwise XOR operator compares each bit of the first operand with the corresponding bit of the second operand, and returns 1 only and only if one of the two bits is 1. It returns 0 if both the bits are 0, and also if both the bits are 1.
For the output to be true, only one of the inputs should exclusively be true. Hence this operator is called as the Exclusive Or operator.
The Truth Table
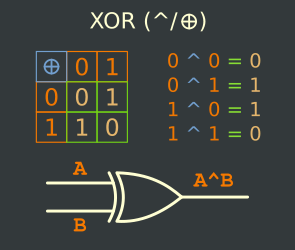
Examples :
28 ^ 12
11100
^ 01100
----------
10000 = 16
12 ^ 16
01100
^ 10000
----------
11100 = 28
28 ^ 16
11100
^ 10000
----------
01100 = 12
Did you notice anything strange in the above examples?
Observe the pattern.
28 ^ 12 = 16
12 ^ 16 = 28
28 ^ 16 = 12
This is a very interesting property of the XOR operator
A ^ B ^ A = B
A ^ B ^ B = A
This specific property forms the base of most of the encryption systems.
Stating it in a very simple terms…
Input ^ Key = Encryption
Encryption ^ Key = Input
XORing Input Data with a Key produces Encrypted data
And, XORing the Encrypted data with the Same Key gives back the Input Data.
In the next article we will look at the Bitwise Shift Operators

